
Astrolander
22 Dec 2018Progress: Complete
I wanted to complete the trilogy, but part of the way through this one I got distracted and started working on the next game. But, there are still a few interesting points to note here.
Lines
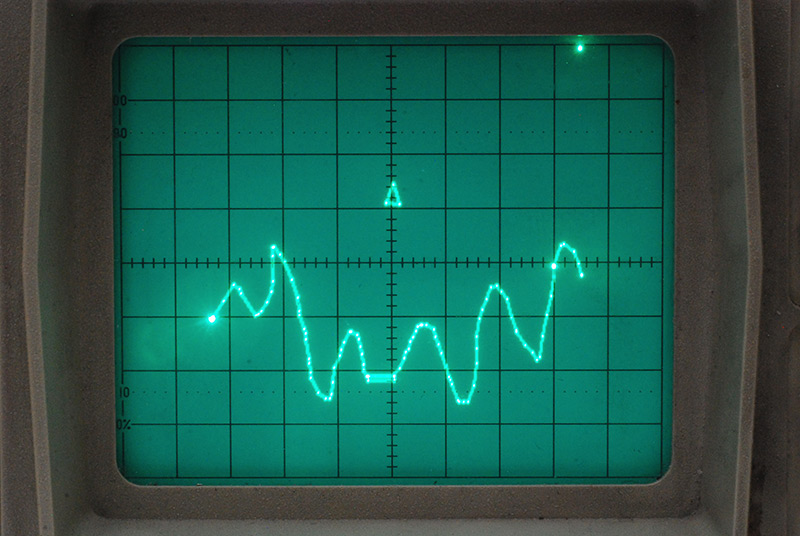
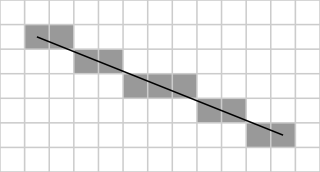
In bitmap graphics, Bresenham's line algorithm is used to draw a straight line between two points.
If you've been looking through the source code so far, you may have been surprised to see the implementation of Bresenham's line algorithm here. Certainly my first thought about vector graphics was that we wouldn't need to worry about this sort of thing, but no, it's actually really important.
Slew rate is the speed at which an output voltage can change. If we tell our video circuit to output a certain value, it will always take a finite amount of time to reach that point. In fact, it'll approach the value exponentially. This is an important point. If we tried to draw a straight line between two points on the display by simply oscillating between the end points, the beam would move exponentially from point to point, and so for anything except 90 or 45 degree angles, instead of a line, we'd end up with a lemon-shape, as the X and Y movements travelled at different speeds.
So we need to use the line algorithm and move a pixel at a time, if we want our lines to be straight. Luckily, it's quite straight forward and I just copied the logic from wikipedia. The real question is, why do old vector games like Asteroids not look pixellated? Well, they are, but they run at a higher resolution so you don't notice it. The real benefit of vector graphics is from the days of limited video memory. With vector graphics, you can have a higher resolution for a given amount of video memory. In our case, however, we were rather silly and went for a low resolution vector output. And also, we have no video memory at all. 90% of our CPU time is spent in the drawing routines.
There is a subtle edge-case in our implementation of the line algorithm. The screen coordinates are all unsigned, but the algorithm works with signed offsets. In order for lines longer than 128 pixels to be drawn correctly, we have to do some extra checking at the start of the routine.
For Astrolander, the example map is something I quickly sketched out in paint, and the points are so close together you that may think the line algorithm isn't needed, but it's all the more important when we start to zoom in on the scene. Also, the real maps, if I ever got as far as ripping them, were mostly composed of straight lines.
Scaling
Acceleration and momentum are pretty much just extensions of what we did with the RetroRacer movement.Scaling means we can't get away with limited resolution, everything needs to be at least 16-bit. With a 16-bit scale factor and 16-bit coordinates, applying the scale means double precision multiplications. Extending the precision of the multiply instructions is a fairly standard proceedure, I think there are even examples of it in the datasheets. It's pretty much a case of high byte times low byte, low byte times high byte, high times high, low times low, and add them all in the right proportions.
; Function scaleCoordinate - modified 16bit signed multiply. ; r21:r20 = scale * r21:r20 scaleCoordinate: push r16 push r17 push r18 push r19 clr r2 muls scaleH, r21 ; (signed)ah * (signed)bh movw r19:r18, r1:r0 mul scaleL, r20 ; al * bl movw r17:r16, r1:r0 mulsu scaleH, r20 ; (signed)ah * bl sbc r19, r2 add r17, r0 adc r18, r1 adc r19, r2 mulsu r21, scaleL ; (signed)bh * al sbc r19, r2 add r17, r0 adc r18, r1 adc r19, r2 sbrs r19,7 ; if result is negative, don't round inc r2 sbrc r17,7 ; round to 16bit result add r18,r2 clr r2 adc r19,r2 movw r21:r20, r19:r18 pop r19 pop r18 pop r17 pop r16 ret
Once we've scaled our coordinate, we then need to only draw it if it's within the display. A modified drawLine routine checks for this, and attempts to draw only part of the line if it's half-in half-out.
I didn't write these games in the order they're presented here, or in the video. I think AstroLander was actually the penultimate game I made, right before mario. Looking through the source code, the style is quite different to how I was writing things at the beginning.
If we'd gotten as far as it, collisions would have been an interesting challenge. We'd really want this to be pixel accurate, so I suppose the only viable way would be to perform a set of comparisons within the line-drawing routines for the terrain. Each pixel in the bresenham implementation would have to be checked against the stack of pixels that compose the triangle that is our spaceship. I'm not sure if we'd have enough processing power for this, but it could probably be inserted in place of the delay routines as it's drawn. As the triangle of the spaceship got bigger, there would be less terrain to check against. Possibly, if needed, a pre-comparison could check if the spaceship is nearby or miles away, and skip the bulk of the code if it isn't needed.
Not much more to be said about this one. Dig in to the juicy, half-finished code below. Commented out is an unfinished auto-scaling routine, but otherwise the zoom is just set by pressing up and down on the controller. Next up, Tetris and the 3D malarky.
### AstroLander.asm ### ;init frame counter ldi r16,0 out TCNT0, r16 ldi r16, (1<<CS02)|(1<<CS01)|(1<<CS00) out TCCR0, r16 ldi r16, 128 out OCR0, r16 .def x_H = r4 .def x_L = r5 .def y_H = r6 .def y_L = r7 .def speedx_H = r8 .def speedx_L = r9 .def speedy_H = r10 .def speedy_L = r11 .def theta = r12 .def translateX = r14 .def translateY = r15 .def scaleH = r22 .def scaleL = r23 ldi scaleH,2 ;2.5 ldi scaleL,128 ldi r16,128 mov translateX,r16 ldi r16,220 mov translateY,r16 ldi r16,0 mov speedx_H,r16 mov speedx_L,r16 mov speedy_H,r16 mov speedy_L,r16 mov x_H,r16 mov y_H,r16 Main: rcall readController ;//////// sbrs r2,ctrlUp rjmp asdf subi scaleL,-1 sbci scaleH,-1 asdf: sbrs r2,ctrlDown rjmp fdsa subi scaleL,1 sbci scaleH,0 fdsa: ;///////// ldi r16, 2 ; turn speed sbrc r2, ctrlLeft add theta,r16 sbrc r2, ctrlRight sub theta,r16 ; Accelerate sbrs r2, ctrlA rjmp doGravity mov r17, theta ldi r16, 16 ; acceleration magnitude rcall sinS ; returns in r1:r0 sbrc r0,7 inc r1 add speedy_L, r1 ldi r16,0 sbrc r1,7 ldi r16,-1 adc speedy_H, r16 mov r17, theta ldi r16, 16 ; acceleration magnitude rcall cosS ; returns in r1:r0 sbrc r0,7 inc r1 add speedx_L, r1 ldi r16,0 sbrc r1,7 ldi r16,-1 adc speedx_H, r16 doGravity: ldi r16,4 add speedy_L,r16 ldi r16,0 adc speedy_H,r16 rcall friction add x_L, speedx_L adc x_H, speedx_H add y_L, speedy_L adc y_H, speedy_H ;push r2 /* ; calculate scaling rcall calcDistance ldi r16,10 cp r1,r16 brcc notclose ;lsl scaleL ;rol scaleH subi scaleL,-8 sbci scaleH,-1 rjmp donescaling notclose: ldi r16,1 ldi r17,0 cp scaleL,r17 cpc scaleH,r16 brcs donescaling ;lsr scaleH ;ror scaleL subi scaleL,8 sbci scaleH,0 donescaling: */ /* ldi ZH, HIGH(scalingLookup*2) ldi ZH, LOW(scalingLookup*2) clr r0 add ZL, r1 adc ZH, r0 add ZL, r1 adc ZH, r0 lpm scaleL, Z+ lpm scaleH, Z+ */ ;pop r2 rcall drawShip ; draw map /* ldi r16,-10 ldi r17,-5 ldi r18,4 ldi r19,-12 ldi r26,0 ldi r27,0 ldi r24,0 ldi r25,0 rcall drawLineScaled */ ldi ZH, HIGH(polygon1*2) ldi ZL, LOW(polygon1*2) rcall drawPolygonPM ldi ZH, HIGH(polygon2*2) ldi ZL, LOW(polygon2*2) rcall drawPolygonPM ldi r16,0 out PORTA,r16 out PORTC,r16 waitforframe: in r16, TIFR sbrs r16, OCF0 rjmp waitforframe ldi r16, (1<<OCF0) out TIFR, r16 ldi r16, 0 out TCNT0, r16 rjmp Main drawShip: push r2 ldi r16,8 mov r17, theta rcall sinS movw r30, r0 ; r31:r30 is now sintheta ldi r16,8 mov r17, theta rcall cosS movw r28, r0 ; r29:r28 is now costheta ; r16 = x0H ; r17 = y0H ; r18 = x1H ; r19 = y1H ; r26 = x0L ; r27 = y0L ; r24 = x1L ; r25 = y1L mov r26,x_L mov r16,x_H add r26,r28 ; x + costheta adc r16,r29 mov r27,y_L mov r17,y_H add r27,r30 ; y + sintheta adc r17,r31 push r16 ; save for later push r17 push r26 push r27 asr r31 ; Halve sin/cos values ror r30 asr r29 ror r28 mov r24,x_L mov r18,x_H add r24,r30 ; x + halfsin - halfcos adc r18,r31 sub r24,r28 sbc r18,r29 mov r25,y_L mov r19,y_H sub r25,r30 ; y -halfcos-halfsin sbc r19,r31 sub r25,r28 sbc r19,r29 rcall drawLineScaled mov r24,x_L mov r18,x_H sub r24,r30 ; x - halfsin - halfcos sbc r18,r31 sub r24,r28 sbc r18,r29 mov r25,y_L mov r19,y_H sub r25,r30 ; y +halfcos-halfsin sbc r19,r31 add r25,r28 adc r19,r29 rcall drawLineScaled pop r25 ; recover starting position pop r24 pop r19 pop r18 rcall drawLineScaled pop r2 sbrs r2,ctrlA rjmp drawShipEnd ; draw the plume mov r26,x_L mov r16,x_H add r27,r30 ; x + halfsin - halfcos adc r16,r31 sub r27,r28 sbc r16,r29 mov r27,y_L mov r17,y_H sub r28,r30 ; y -halfcos-halfsin sbc r17,r31 sub r28,r28 sbc r17,r29 mov r24,x_L ; x-costheta mov r18,x_H sub r24,r28 sbc r18,r29 sub r24,r28 sbc r18,r29 mov r25,y_L mov r19,y_H sub r25,r30 ; y -sintheta sbc r19,r31 sub r25,r30 sbc r19,r31 rcall drawLineScaled mov r24,x_L mov r18,x_H sub r24,r30 ; x - halfsin - halfcos sbc r18,r31 sub r24,r28 sbc r18,r29 mov r25,y_L mov r19,y_H sub r25,r30 ; y +halfcos-halfsin sbc r19,r31 add r25,r28 adc r19,r29 rcall drawLineScaled drawShipEnd: ret ; Function friction ; subtracts one sixteenth of current speed from speed friction: push r16 push r17 clr r17 sbrc speedx_H,7 dec r17 mov r16, speedx_H sub speedx_L, r16 sbc speedx_H,r17 clr r17 sbrc speedy_H,7 dec r17 mov r16, speedy_H sub speedy_L, r16 sbc speedy_H,r17 pop r17 pop r16 ret ; function calcDistance ; Works out the squared distance between x_H,y_H and 0,0 calcDistance: ;ldi r16,0 ;ldi r17,0 mov r26,x_H ;sub r26,r16 ; Difference between x coordinates muls r26,r26 ; square it movw r24,r0 ; save for later mov r26,y_H ;sub r26,r17 ; difference in y coordinates muls r26,r26 ; square it add r0,r24 ; add two values together adc r1,r25 ; (return in r1:r0) ret ; Function scaleCoordinate - modified 16bit signed multiply. ; r21:r20 = scale * r21:r20 scaleCoordinate: push r16 push r17 push r18 push r19 clr r2 muls scaleH, r21 ; (signed)ah * (signed)bh movw r19:r18, r1:r0 mul scaleL, r20 ; al * bl movw r17:r16, r1:r0 mulsu scaleH, r20 ; (signed)ah * bl sbc r19, r2 add r17, r0 adc r18, r1 adc r19, r2 mulsu r21, scaleL ; (signed)bh * al sbc r19, r2 add r17, r0 adc r18, r1 adc r19, r2 sbrs r19,7 ; if result is negative, don't round inc r2 sbrc r17,7 ; round to 16bit result add r18,r2 clr r2 adc r19,r2 movw r21:r20, r19:r18 pop r19 pop r18 pop r17 pop r16 ret /* ; Transform functions - scale and translate. transformX: mov r21,x_H mov r20,x_L rcall scaleCoordinate add r20,translateX adc r21,r2 ret transformY: mov r21,y_H mov r20,y_L rcall scaleCoordinate add r20,translateY adc r21,r2 ret */ /* Function drawPolygonPM(Z pointer) * Draw from a list of coords in program memory * First byte is number of vertices, followed by pairs of x,y bytes */ drawPolygonPM: .def vertexCount=r3 lpm vertexCount, Z+ lpm r16,Z+ ; load starting point lpm r17,Z+ ; all polygons must have at least 2 vertices dec vertexCount polyPMnextVert: lpm r18,Z+ ; load next vertex lpm r19,Z+ ldi r26,0 ldi r27,0 ldi r24,0 ldi r25,0 rcall drawLineScaled dec vertexCount brne polyPMnextVert ; repeat until end of polygon ret drawLineScaled: ; Transform start and end coordinates. ; If within the screen, call ordinary drawLine. ; r16 = x0H ; r17 = y0H ; r18 = x1H ; r19 = y1H ; r26 = x0L ; r27 = y0L ; r24 = x1L ; r25 = y1L push r18 ; save final coordinate push r19 push r24 push r25 ; scale x0 mov r21,r16 mov r20,r26 rcall scaleCoordinate add r20,translateX adc r21,r2 cpi r21, 0 breq dLx0WithinRange ; x0 is out of range rjmp scaleLine dLx0WithinRange: push r20 ; x0 ok ; scale y0 mov r21, r17 mov r20, r27 rcall scaleCoordinate add r20,translateY adc r21,r2 cpi r21,0 breq dLy0WithinRange ; y0 is out of range pop r20 rjmp scaleLine dLy0WithinRange: push r20 ; scale x1 mov r21,r18 mov r20,r24 rcall scaleCoordinate add r20,translateX adc r21,r2 cpi r21, 0 breq dLx1WithinRange ; x1 is out of range pop r20 pop r20 rjmp scaleLine dLx1WithinRange: push r20 ; scale y1 mov r21, r19 mov r20, r25 rcall scaleCoordinate add r20,translateY adc r21,r2 cpi r21,0 breq dLy1WithinRange ; y1 is out of range pop r20 pop r20 pop r20 rjmp scaleLine dLy1WithinRange: mov r19,r20 pop r18 pop r17 pop r16 rcall drawLine scaleLine: ; for now, just don't draw it. pop r27 ;shift end point to starting point (for polygons) pop r26 pop r17 pop r16 ret /* ;Local variables push r20 push r21 push r22 push r23 push r24 push r25 .def slowx=r20 .def slowy=r21 .def fastx=r22 .def fasty=r23 .def err = r24 .def t = r25 ; First we split the magnitude and direction ; Need to be careful/explicit because mag could be >127 cp dx,x0 breq slineXeq brcs slineXneg ; Carry flag set if it overflowed ldi slowx,1 ; slowx is the direction sub dx,x0 ; dx is now the magnitude rjmp slineY slineXneg: ldi slowx,-1 mov t, x0 ; t as temp var sub t, dx mov dx, t rjmp slineY slineXeq: clr slowx clr dx slineY: ; Now do the same for y cp dy,y0 breq slineYeq brcs slineYneg ldi slowy,1 sub dy,y0 rjmp slineCheckDistance slineYneg: ldi slowy,-1 mov t, y0 ; t as temp var sub t, dy mov dy, t rjmp slineCheckDistance slineYeq: clr slowy clr dy slineCheckDistance: ; Now to find which direction is "faster" cp dx, dy brcs slineDxLessthanDy mov fastx, slowx ; x is the fast direction clr fasty eor dx, dy ; Tripple XOR, the classy way to eor dy, dx ; swap two registers eor dx, dy rjmp slineInit slineDxLessthanDy: mov fasty, slowy ; y is the fast direction, no need to swap clr fastx slineInit: mov err, dy ; set err to half the furthest distance lsr err out PORTA, x0 ; We are now ready to draw the line out PORTC, y0 rcall delayPixel mov t, dy slineNextPixel: sub err, dx ; Update error term brcc slineStepParallel add err, dy ; Make error term positive again add x0,slowx ; Step diagonally add y0,slowy rjmp slineLoopBack slineStepParallel: add x0,fastx ; Step parallel add y0,fasty slineLoopBack: out PORTA, x0 ; Plot point out PORTC, y0 rcall delayPixel dec t brne slineNextPixel pop r25 pop r24 pop r23 pop r22 pop r21 pop r20 ret ; End of drawLine */ /* Function drawLine (x0,y0,x1,y1) * My implementation of Bresenham line algorithm * based on pseudocode/description from wikipedia */ drawLine: ;Function arguments .def x0=r16 .def y0=r17 .def dx=r18 .def dy=r19 ;Local variables push r20 push r21 push r22 push r23 push r24 push r25 .def slowx=r20 .def slowy=r21 .def fastx=r22 .def fasty=r23 .def err = r24 .def t = r25 ; First we split the magnitude and direction ; Need to be careful/explicit because mag could be >127 cp dx,x0 breq lineXeq brcs lineXneg ; Carry flag set if it overflowed ldi slowx,1 ; slowx is the direction sub dx,x0 ; dx is now the magnitude rjmp lineY lineXneg: ldi slowx,-1 mov t, x0 ; t as temp var sub t, dx mov dx, t rjmp lineY lineXeq: clr slowx clr dx lineY: ; Now do the same for y cp dy,y0 breq lineYeq brcs lineYneg ldi slowy,1 sub dy,y0 rjmp lineCheckDistance lineYneg: ldi slowy,-1 mov t, y0 ; t as temp var sub t, dy mov dy, t rjmp lineCheckDistance lineYeq: clr slowy clr dy lineCheckDistance: ; Now to find which direction is "faster" cp dx, dy brcs lineDxLessthanDy mov fastx, slowx ; x is the fast direction clr fasty eor dx, dy ; Tripple XOR, the classy way to eor dy, dx ; swap two registers eor dx, dy rjmp lineInit lineDxLessthanDy: mov fasty, slowy ; y is the fast direction, no need to swap clr fastx lineInit: mov err, dy ; set err to half the furthest distance lsr err out PORTA, x0 ; We are now ready to draw the line out PORTC, y0 rcall delayPixel mov t, dy lineNextPixel: sub err, dx ; Update error term brcc lineStepParallel add err, dy ; Make error term positive again add x0,slowx ; Step diagonally add y0,slowy rjmp lineLoopBack lineStepParallel: add x0,fastx ; Step parallel add y0,fasty lineLoopBack: out PORTA, x0 ; Plot point out PORTC, y0 rcall delayPixel dec t brne lineNextPixel pop r25 pop r24 pop r23 pop r22 pop r21 pop r20 ret ; End of drawLine delayPixel: push r16 ldi r16,12 delayPixelLoop: dec r16 brne delayPixelLoop pop r16 ret /* Function sinS(coordinate, dir) * Scales 8bit signed coordinate by sine of the direction * Simplified, no rounding, returns in r1:r0 */ sinS: .def cor=r16 .def dir=r17 push ZH push ZL ldi ZH, HIGH(sineTable*2+255) ldi ZL, LOW(sineTable*2+255) sub ZL, dir sbci ZH, $00 ; sub-with-carry 0 from high byte lpm dir, Z fmuls cor,dir pop ZL pop ZH ret /* Function cosS(coordinate, dir) * Scales 8bit signed coordinate by cosine of the direction */ cosS: push ZH push ZL ldi ZH, HIGH(sineTable*2+255) ldi ZL, LOW(sineTable*2+255) ; reuse table, but shift by pi/2 subi dir, 192 ; which in our notation is 64 (-192) sub ZL, dir sbci ZH, $00 lpm dir, Z fmuls cor,dir pop ZL pop ZH ret ; Function readController, loads into r2 readController: sbis SPSR,SPIF rjmp readController ; Wait for reception complete in r2,SPDR ; Read received data com r2 push r16 ldi r16,0b00000000 ; init controller read again out SPDR,r16 pop r16 ret ; signed values, in reverse order sineTable: .db $FD,$FA,$F7,$F4,$F0,$ED,$EA,$E7,$E4,$E1,$DE,$DB,$D8,$D5,$D2,$CF,$CD,$CA,$C7,$C4,$C1,$BF,$BC,$B9,$B7,$B4,$B2,$AF,$AD,$AB,$A8,$A6,$A4,$A2,$A0,$9E,$9C,$9A,$98,$96,$95,$93,$91,$90,$8F,$8D,$8C,$8B,$8A,$88,$87,$86,$86,$85,$84,$83,$83,$82,$82,$82,$81,$81,$81,$81,$81,$81,$81,$82,$82,$82,$83,$83,$84,$85,$86,$86,$87,$88,$8A,$8B,$8C,$8D,$8F,$90,$91,$93,$95,$96,$98,$9A,$9C,$9E,$A0,$A2,$A4,$A6,$A8,$AB,$AD,$AF,$B2,$B4,$B7,$B9,$BC,$BF,$C1,$C4,$C7,$CA,$CD,$CF,$D2,$D5,$D8,$DB,$DE,$E1,$E4,$E7,$EA,$ED,$F0,$F4,$F7,$FA,$FD,$00,$03,$06,$09,$0C,$10,$13,$16,$19,$1C,$1F,$22,$25,$28,$2B,$2E,$31,$33,$36,$39,$3C,$3F,$41,$44,$47,$49,$4C,$4E,$51,$53,$55,$58,$5A,$5C,$5E,$60,$62,$64,$66,$68,$6A,$6B,$6D,$6F,$70,$71,$73,$74,$75,$76,$78,$79,$7A,$7A,$7B,$7C,$7D,$7D,$7E,$7E,$7E,$7F,$7F,$7F,$7F,$7F,$7F,$7F,$7E,$7E,$7E,$7D,$7D,$7C,$7B,$7A,$7A,$79,$78,$76,$75,$74,$73,$71,$70,$6F,$6D,$6B,$6A,$68,$66,$64,$62,$60,$5E,$5C,$5A,$58,$55,$53,$51,$4E,$4C,$49,$47,$44,$41,$3F,$3C,$39,$36,$33,$31,$2E,$2B,$28,$25,$22,$1F,$1C,$19,$16,$13,$10,$0C,$09,$06,$03,$00 polygon2: .db 63, 0,0,-3,-3,-6,-10,-7,-13,-9,-15,-10,-20,-11,-22,-13,-26,-14,-29,-16,-30,-17,-30,-20,-30,-24,-27,-25,-22,-27,-18,-29,-12,-31,-4,-33,2,-34,4,-35,6,-39,16,-40,17,-42,17,-45,17,-49,7,-51,-6,-51,-15,-51,-22,-52,-33,-54,-39,-57,-45,-60,-52,-63,-53,-66,-50,-70,-45,-72,-34,-75,-26,-75,-25,-81,-17,-85,-12,-88,-8,-90,-10,-92,-22,-94,-35,-97,-47,-99,-59,-99,-65,-99,-65,-99,-66,-103,-78,-105,-79,-112,-74,-114,-67,-116,-60,-119,-48,-120,-38,-121,-29,-121,-17,-123,-11,-124,-8,-125,-7,-126,-4,-128,-3 polygon1: .db 55, 0,1,16,1,16,4,0,4,0,1,17,1,19,-2,19,-6,20,-12,21,-17,22,-21,23,-24,26,-26,27,-26,31,-20,33,-15,34,-11,37,-4,38,5,39,12,40,15,43,15,47,11,52,2,52,-1,53,-7,53,-10,55,-21,55,-25,56,-28,58,-36,58,-39,59,-47,63,-58,67,-69,70,-73,74,-78,75,-78,75,-72,75,-57,76,-51,78,-44,82,-39,84,-37,86,-36,95,-50,96,-52,99,-55,106,-45,113,-34,113,-34,113,-34,122,-33,125,-36,127,-41 .include "Bootloader.asm"
Marvellous. Continue to page 9.