

| anyfoo | Posted: 20 May 2022, 04:15 AM |
|---|---|
|
Member Posts: 4 Joined: 6-May 22 |
I thought you might like this, done in a bored afternoon. It's a little shell oneliner that is ultimately an exercise in LSFR, simple IIR filters, and fixed point arithmetic, but with the neat twist that it can be entirely worked out without a computer (and no filter design etc.), and theoretically even without a calculator, entirely on paper. Though I admit I was a bit lazier than that. Needs zsh and an xterm-like terminal that does true color (Terminal.app on macOS is fine). Detailed explanation below. I know that mitxela knows at least some of this subject matter, the explanation was written for a more general audience. Writing it down was fun, I should get my own blog. echo -ne '\e[8;32;90;t';n=20;t=524292;l=$((t-1));m=$((2**n-1));c=0;xs=(1);ys=(1);for ((i=0;i<n*m;i++));do b=$((l&1));l=$(((l>>1)^(b*t)));c=$(((c<<1|b)&m));[ $((i%n)) -eq 0 ] &&{xs=($c $xs[1,4]);y=$((((xs[4]-xs[0])<<30-0x3fffd60f*ys[2]+0x7d32617c*ys[1])>>30));ys=($y $ys[1]);yd=$((120+(y >> 24)));printf '\e[48;5;%um ' $yd};doneDisclaimer for everyone reading: Never just run code like this. I have given you what is essentially gibberish for you to paste in a shell, and without close inspections there is no telling what this could do to your computer. It's a harmless piece of code, but everyone can just say that. Instead, closely inspect it, run it in an isolated vm, or, you know, just watch this video that I took of it running. So let's go through what it actually does. I will skip the looping and actual printing (echo/printf). n=20;t=524292;l=$((t-1));m=$((2**n-1)); ... b=$((l&1));l=$(((l>>1)^(b*t)));c=$(((c<<1|b)&m)) This is just a 20 bit LFSR. Essentially, just a very cheap way of getting pseudo-random data. zsh has the ability to give us that by itself, but I wanted the whole thing to be "no external input at all", and the code for the LFSR adds a bit to the mystery. LFSRs are widely documented and not the interesting part, so I'll leave it at that. If we did directly output the LFSR's output as colored patches, we'd just get colorful noise, which is much less interesting. Instead, we do this to each value: xs=($c $xs[1,4]);y=$((((xs[4]-xs[0])<<30-0x3fffd60f*ys[2]+0x7d32617c*ys[1])>>30));ys=($y $ys[1]);yd=$((120+(y >> 24))) This is the core of the effect. It's just a very simple peak filter, an IIR filter specifically. The angular frequency of the peak is a near but not exact multiple of my terminal width, and this is how we get those slightly moving bands. As an IIR filter, it just consists of adding together past inputs and outputs, after multiplying each of them with a coefficient, and nothing more. Would it only use past inputs, it would be an FIR filter. FIR filters have a few advantages that don't matter here, and they would also need many more coefficients. But most importantly, this IIR filter was extremely easy to design from scratch, with only knowledge of the z transform: I did not use any parametrical filter design to find the coefficients or similar. Instead, I simply placed some trivial zeroes and a single pole (actually a conjugate pair, since it's a real filter) in the z plane. The pole sits at the angular frequency I want, but just ever so slightly inside the unit circle. You can see the pole (the two "x"s on the right side of the graph) barely approaching the unit circle: 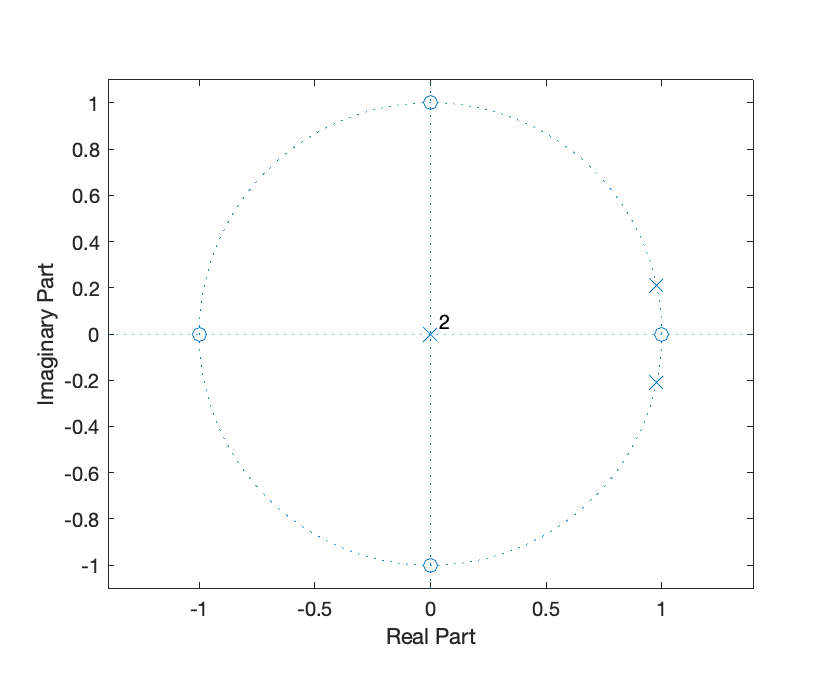 Get the coordinates of your zeroes and poles in rectangular form, put the zeroes into the nominator, the poles into the denominator, and that is your transfer function: 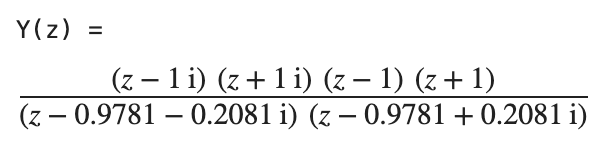 Expand both nominator and denominator by multiplication to obtain polynomial form: 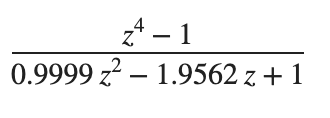 There are other ways to do this by hand, but they require you to know or derive more complicated formulas. You can also do all these steps completely without any software. A calculator may be handy to convert polar coordinates into rectangular coordinates and for multiplying, but you could also eyeball the rectangular coordinates, and the multiplication is well feasible on paper. That's a very simple transfer function, and by the nature of z transforms and how they relate to difference equations, we can pretty much directly read off the difference equation for our shell script. Still no software needed. In our case that would be: y(n) = x(n-4)-x(n)-0.99999*y(n-2)+1.9562*y(n) And that's our filter. But wait, let's look at the equation that is actually in the script: y=$((((xs[4]-xs[0])<<30-0x3fffd60f*ys[2]+0x7d32617c*ys[1])>>30)) This has the right structure if you squint, but those numbers look nothing like our coefficients. Why are they weirdly large hexadecimal numbers, and what's with those shifts? Well, the coefficients we figured out with pen and paper are not integers, but real numbers. Now we could use floating point math, and zsh specifically (not all shells!) supports this. And indeed, if we just write: y=$((xs[4]-xs[0]-0.99999*ys[2]+1.9562*ys[1])) Then this does work as expected, and is now fully recognizable. But it's also... icky. It's just so unnecessary to use floating point for a simple filter in a simple application. It's often icky to use floating point generally in many applications. You either need an FPU or some other hardware that does floating point, or do some awfully slow floating point emulation in software. All for no good reason. The boring way to talk about this would be to just say that we scaled the coefficients up and the result back down, but that's really boring, and while it's functionally the same, the following can be easier to reason about than scaling steps. So let's in fact not just call what we did scaling, and instead talk about Fixed Point Arithmetic. The trick is to just designate a number of bits to represent the part before the decimal point, and the rest to be the part after. We are in a binary system here, not decimal, so the (binary) digits after the decimal point are not how many 1/10th, 1/100th, 1/1000th etc. are in the number like we're used to, but how many 1/2, 1/4, 1/8th and so on (and this being binary, it's either one or none of each of those). It's also now a "binary point" instead of a decimal point, so let's less confusingly talk about the part before the point as the "integer" part, and the part after the point as the "fractional" part. This is actually very intuitive to work with. Take the binary numbers "10" and "11". Taking both digits as being part of the integer part, so no fractional part, those are simply the decimal numbers 2 and 3. If you define that only the first digit is integer, and the second the fractional part, then it is 1 and 1.5 respectively. 00 and 01 are 0 and 0.5 respectively. For 101, if the first two digits are integer, then it's 2.5 in decimal. If only the first digit is integer, then it's 1.25. Binary 0001 with zero integer bits, so all fractional bits, is 1/16, so that's 0.0652. You get the idea. It's like seeing all prices in pences with no fraction, instead of pounds with two decimal digits, but in binary and with arbitrary widths. (You can even have more fractional bits than total bits. Let's assume for example that all your numbers are below 0.25. Not only do you not need an integer part, you also don't need the bit for 1/2 = 0.5, as well as the bit for 1/4 = 0.25. So you can have, let's say, 16 total bits with 18 fractional bits, and the not-existing first two bits for 0.5 and 0.25 are inaccessible and always 0, still allowing you to represent any number below 0.25 with 16 bit accuracy. This also works the other way, more integer bits than total bits, where your integer range gets larger but you lose the ability to represent all integers. For example, 7 total bits with 8 integer bits still gives you numbers between 0 and 255, but now only the even ones.) The thing to realize is that binary arithmetic does not care whether there is a "binary point", and if so where it is, i.e. where the integer part ends and the fractional part begins. Add or multiply 100110 and 011010, and no matter how many digits make up what part, the equation always works out. The only thing to remember is that the number of fractional bits always stays the same after any such operation, i.e. the point is always at the same place, it never moves. Hence it is a "fixed" point. You can, however, shift your binary number left or right to essentially convert it into a different fixed point representation, which then has one more or one less bit in the fractional part respectively. We will use that later on. So let's try to fit our coefficients in 32 bits, as that's a reasonable size for our application. The largest number we encounter is 1.9562. We only need one bit to represent our integer part, as it's at most 1. The rest, we could entirely dedicate to the fractional part, but let's add in a sign bit to allow for negative coefficients. (Well, that was my original plan, in the end I just ended up flipping the operation for negative coefficients, so that sign bit is wasted). For 32 bits that means 1 sign bit, 1 integer bit, and the last 30 bits are fractional. Integer numbers with no fractional part can just be shifted 30 bits to the left to convert into our 1:30 representation, and this is what we do above for x(n-4) and x(n), which effectively have 1 as their coefficient: xs[4]<<30 - xs[0]<<30 or (xs[4]-xs[0])<<30 To get our non-integer coefficient in our 1:30 fixed point representation, shifting those numbers would be a bit ill-defined. We would have to do it in fixed point representation, but this is exactly what we are trying to construct here. Floating point numbers have an entirely different internal representation (with mantissa and exponent), so representing our coefficient in C or JavaScript's floating point format and shifting that would be largely nonsensical. But shifting an integer 30 bits to the left is the same as multiplying it by 2^30, and so we do that to get to our fixed point number. (It makes intuitive sense if you see the fixed point representation not as separate "integer and fractional part" in this case, but as an integer number that says "how much of the entire range do we have". We are after all scaling by 2^n, but we don't call it scaling, we are calling it conversion to another fixed point representation.) So for our numbers: 2^ 30 = 1073741824 = 0x40000000 Note that we rounded the decimal results of the multiplications, as we want these to be integer 32 bit numbers (which from now on will represent fixed point numbers in 1:30 format). And now we have it: y=$((((xs[4]-xs[0])<<30-0x3fffd60f*ys[2]+0x7d32617c*ys[1])>>30)) There is one crucial last step in the above, which is shifting the result back 30 bits to the right. This transforms/scales it back into the old familiar integer representation. Doesn't that mean that we just cut the fractional part off entirely? Yes! Fortunately though, the input from the LFSR was a large 20 bit integer number (with one bit actually being the sign bit). The gain of our filter is (nearly enough) 1, so the output is in the same order of magnitude. That being the case, the fractional part of the output is really insignificant. We could even cut off more. This also means that we need zsh to use 64 bit numbers internally, or rather at least 20+32 bits, otherwise our multiplications would be constantly overflowing. If we wanted to maximize our capabilities, we'd make our coefficients fit in 64-20 = 44 bits. 32 bits was already overkill, however. So there you have it. A short oneliner making a pretty and strangely "analogue" but stable pattern, with no external input, all of which can easily be designed on paper. I thought it was fun. Last edit by anyfoo at 20 May 2022, 06:59 AM ------------- |
| [top] | |
| mit | Posted: 20 May 2022, 11:17 AM |
|
yeah whatever Admin Posts: 660 Joined: 4-May 16 |
Marvellous! Thanks for sharing, I enjoyed reading that. First thing this reminds me of is Dwitter -https://www.dwitter.net/ - which is a site where people make visual demos using very short chunks of javascript. Some of them are unbelievable. Very few of them have explanations as detailed as yours. Another thing it reminds me of, music from very short c programs: https://www.youtube.com/watch?v=GtQdIYUtAHg I get the feeling these were mostly discovered by accident, rather than on paper. Oh, also, a chance to plug my fractional base translator which is for floats, but still fun to play with. ------------- |
| [top] | |
| anyfoo | Posted: 22 May 2022, 07:44 PM |
|
Member Posts: 4 Joined: 6-May 22 |
Neat. Tried to write the same thing in a dwitter yesterday, but failed to get it to 140 characters. It's not even so much that I couldn't shorten the shell oneliner down, but that dwitter is fundamentally different from how I output here (and those fillStyle and fillRect are very long). Doesn't mean that it wouldn't be possible though, I barely know any JavaScript. The music is remarkable. Reminds me of cat'ing the Linux kernel into /dev/snd many years ago, but these C programs are more regular and tuned or at the very least selected for good sound, so it's definitely more listenable. The arbitrary base number translator seems useful. I wonder if I actually have anything else that can do that. ------------- |
| [top] | |
| mit | Posted: 25 May 2022, 09:08 AM |
|
yeah whatever Admin Posts: 660 Joined: 4-May 16 |
Yeah, I've never tried dwitter but it's certainly a different output format... and way of thinking. They've defined a handful of helper functions (like S() being Math.sin()) to help keep the lengths down. There's also the somewhat distracting, slightly cheating way of encoding the script in binary and calling eval/unescape stuff. Having a full canvas to draw on does seem like a bit too much freedom compared to piping the output to a terminal or whatever. I just noticed that the author of the music from short programs video has a blog post about it: https://countercomplex.blogspot.com/2011/10/algorithmic-symphonies-from-one-line-of.html ------------- |
| [top] | |
Sign in to post a reply.